Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và co...

Question

Cho hàm số $y = f left x...

0

Cho hàm số

y = f\left( x \right)

liên tục trên

\mathbb{R}

và có đồ thị như hình vẽ bên. Hình phẳng được đánh dấu trong hình bên có diện tích là

\int\limits_a^b {f(x)} dx - \int\limits_b^c {f(x)} dx

\int\limits_a^b {f(x)} dx + \int\limits_b^c {f(x)} dx

- \int\limits_a^b {f(x)} dx + \int\limits_b^c {f(x)} dx

\int\limits_a^b {f(x)} dx - \int\limits_c^b {f(x)} dx

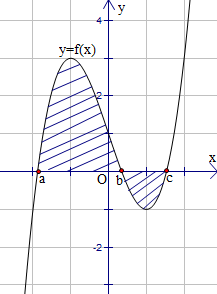
Gửi 6 năm trước

Mới nhất Cũ nhất Phiếu bầu

Nguyễn Khánh · Accepted Answer · 2019-01-03T15:09:46.000Z

0

Đáp án đúng của câu này là:

\int\limits_a^b {f(x)} dx - \int\limits_b^c {f(x)} dx

Nguyễn Khánh

Gửi 6 năm trước

Thêm bình luận