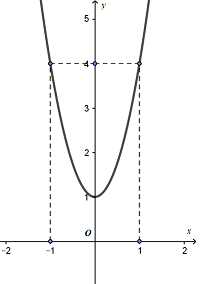
Cho hàm số $y = f(x) = a{x^3} + b{x^2} + cx + d{\text{ }}\left( {a,b,c,d \in \mathbb{R},a \ne 0} \right)$ có đồ thị là $\left( C \right)$. Biết rằng đồ thị $\left( C \right)$ đi qua gốc tọa độ và đồ thị hàm số $y = f'(x)$ cho bởi hình vẽ bên. Tính giá trị $H = f(4) - f(2)$?
Gửi 5 năm trước